[선형대수학] 📂. 벡터(Vector)
1. 벡터(Vector)
1.1 공학과 수학에서의 벡터 : n-공간
- 스칼라(
scalar) :크기만 주어지지만 완전히 표시되는 양 - 벡터(
vector) :크기뿐만 아니라방향까지 지정하지 않으면 완전히 표현할 수 없는 양
- 2차원, 3차원 공간의 벡터는화살표로 표현 가능하다.
- 시작점과 끝점이 같아 크기가 0인 벡터를영벡터라 한다.
- 벡터는크기와방향이같으면시작점에 관계없이 항상동일한 벡터로 간주한다.
- 모든 벡터는점의 좌표를 이용하여 나타낼 수 있다.
- 덧셈, 뺄셈
- $x+y$는 $x, y$에 의하여 결정되는
평행사변형의 대각선으로 표시되는 벡터이다.
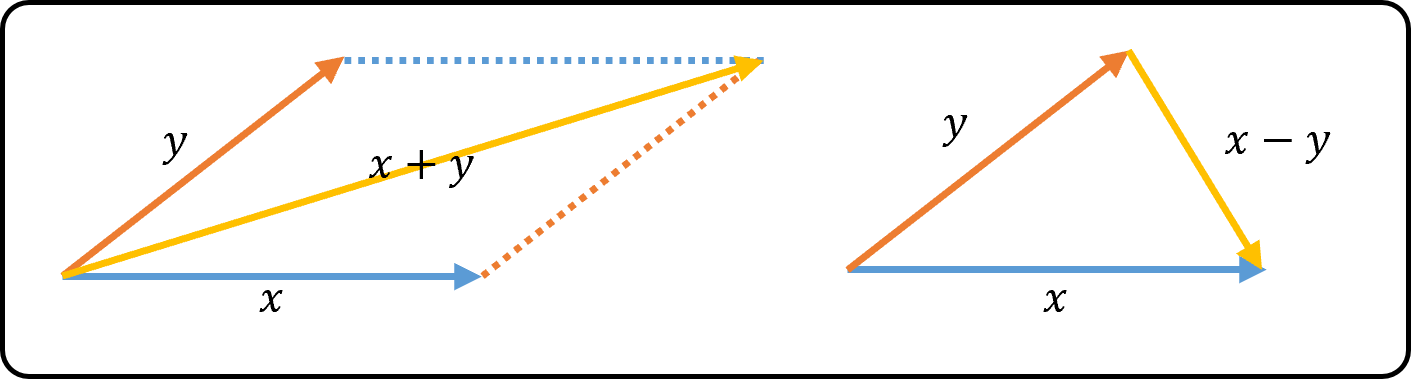
- $x+y$는 $x, y$에 의하여 결정되는
- 스칼라배
- $k>0$이면, $x$와
방향이 같으면서 길이는 $k$배하여 얻어지는 벡터. - $k<0$이면, $x$와
방향이 반대면서 길이는 $\lvert k \rvert$배하여 얻어지는 백터. - $\mathrm{x}=k\mathrm{y}$이면, $\mathrm{x}$와 $\mathrm{y}$는
평행하다.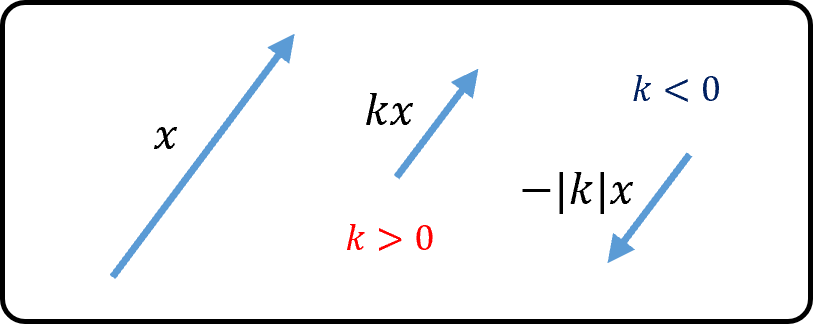
- $k>0$이면, $x$와
- n차원 벡터
$n$개의 실수의 순서조$(x_1, x_2, \dots, x_n)$을
n차원 벡터(n-demensional vector)라 하고
\(\mathrm{x}=(x_1, x_2, \dots, x_n)=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}_{n\times1}\)
로 나타낸다. 이때 실수 $x_1, x_2, \dots, x_n$을 $x$의성분이라 한다.
- 상등
$\mathbb{R}^n$의 벡터
\(\mathrm{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix},\mathrm{y}=\begin{bmatrix}y_1\\y_2\\\vdots\\y_n\end{bmatrix}\) 에 대하여 $x_i=y_i$ $(i=1,2, \dots, n)$이면, $x=y$라고 한다.- $(1)\mathrm{x}\pm\mathrm{y}=\begin{bmatrix}x_1\pm y_1 \\ x_2\pm y_2 \\ \vdots \\ x_n\pm y_n\end{bmatrix}(2)k\mathrm{x}=\begin{bmatrix}kx_1 \\ kx_2 \\ \vdots \ kx_n\end{bmatrix}$
- 일차결합
$v_1, v_2, \dots, v_k$가 $\mathbb{R}^n$의 벡터이고, 계수 $c_1, c_2, \dots, c_k$가 실수일 때,
\(\mathrm{x}=c_1v_1+c_2v_2+ \dots + c_kv_k\)
인 형태를 $v1,v2,\dots,v_k$의일차결합(linear combination)이라 한다.
1.2 내적과 직교
- 노름
$\mathbb{R}^n$의 벡터 $x=(x_1, x_2, \dots, x_n)$에 대하여
\(\|\mathrm{x}\|=\sqrt{x_1^2+x_2^2+ \dots + x_n^2}\)
을 $x$의노름(norm, length magnitude)이라 한다.원점에서 점 $P(x_1, x_2, \dots, x_n)$에 이르는거리이다.- 두 벡터의 거리
\(\|\mathrm{x}-\mathrm{y}\|=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\dots+(x_n-y_n)^2}\) 단위벡터(unit vector)
\(\|\mathrm{x}\|=1, \; \mathrm{u}=\frac{1}{\|\mathrm{x}\|}\mathrm{x}\)
- 내적
$\mathbb{R}^n$의 벡터 $\mathrm{x}=(x_1,x_2,\dots,x_n)$와 $\mathrm{y}=(y_1,y_2,\dots,y_n)$에 대하여,
\(\mathrm{x}\cdot\mathrm{y}=x_1y_1+x_2y_2+\dots+x_ny_n\)
\(\mathrm{x}\cdot\mathrm{y}=\|\mathrm{x}\|\|\mathrm{x}\|\cos{\theta},\;0\le\theta\le\pi\)
내적(Euclidean inner product, dot product)이라 한다.- $\mathrm{x}\cdot\mathrm{x}=|\mathrm{x}|^2$
- $\mathrm{x}\cdot\mathrm{x}\ge0,\; \mathrm{x}\cdot\mathrm{x}=0\Leftrightarrow \mathrm{x}=0$
- $\mathrm{x}\cdot\mathrm{y} = \mathrm{y}\cdot\mathrm{x}$
- $(\mathrm{x}+\mathrm{y})\cdot\mathrm{z}=\mathrm{x}\cdot\mathrm{z}+\mathrm{y}\cdot\mathrm{z}$
- $(k\mathrm{x})\cdot\mathrm{y}=\mathrm{x}\cdot(k\mathrm{y})=k(\mathrm{x}\cdot\mathrm{y})$
- $\mathrm{x}\cdot\mathrm{y}=0$이면, $\mathrm{x}$와 $\mathrm{y}$는
직교한다. (직교벡터)
- 코시-슈바르츠 부등식(Cauchy-Schwarz Inequality)
$\mathbb{R}^n$의 임의의 벡터 $\mathrm{x}$ $\mathrm{y}$에 대하여 다음 부등식이 성립한다.
\(|\mathrm{x}\cdot\mathrm{y}|\le\|\mathrm{x}\|\|\mathrm{y}\|\)
단, 등호는 $\mathrm{x}$, $\mathrm{y}$ 중 하나가 다른 것의실수배일 때만 성립한다.- 증명
- 삼각부등식
\(\|\mathrm{x}+\mathrm{y}\|\le\|\mathrm{x}\|\|\mathrm{y}\|\) - 단, 등호는 $\mathrm{x}$, $\mathrm{y}$ 중 하나가 다른 것의 $k\ge0$배일 때만 성립한다.
- 삼각부등식
- 증명
정규직교(orthonormal)벡터$\mathrm{x}$, $\mathrm{y}$가 서로
직교벡터이면서단위벡터인 벡터기본단위벡터(standard unit vector, 표준단위벡터)\[\mathrm{e}_1=(1,0,0,\dots,0),\mathrm{e}_2=(0,1,0,\dots,0),\dots,\mathrm{e}_n=(0,0,0,\dots,1)\]

댓글남기기