[선형대수학] 📂. 행렬식(Determinant)

1. 행렬식의 정의와 기본정리

치환 (Permutation)

• 자연수의 집합 $S={1, 2, 3, \dots, N}$의 치환(permutation, 순열) : $S$에서 $S$로의 1:1대응 함수
  \(\delta=( \delta(1), \delta(2), \dots, \delta(n) )=(i_1, i_2, \dots, i_n)\)
  

  ---

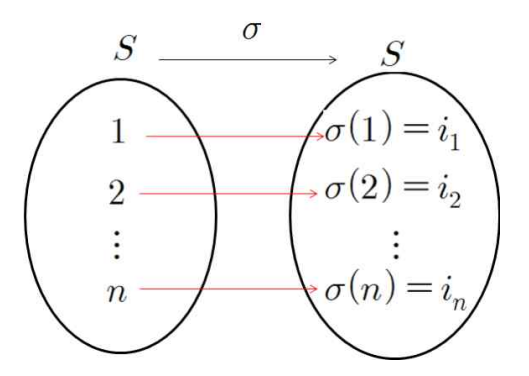
  • $S_n$ : 집합$S$의 모든 치환의 집합 표시
  • $S={1, 2, \dots, n}$의 치환의 개수 : $n!$

반전(Inversion)

• 큰 자연수가 작은 자연수보다 더 왼쪽에 먼저 나타나는 경우
  \((j_1, j_2, \dots, j_k, \dots, j_i, \dots, j_n), (j_k > j_i)\)

반전수

• j_k에 대한 반전수 : j_k보다 작은 수의 개수
  $\delta$의 반전수 = $j_1$의 반전수 + $j_2$의 반전수 + $\dots$ + $j_n$의 반전수

  ---

  1. 짝치환(even permutation) : 치환의 반전수가 짝수
  2. 홀치환(odd permutation) : 치환의 반전수가 홀수

부호화 함수(signature function)

• 치환의 부호를 결정
  \(sgn(\delta)=\begin{cases}+1 & (\delta : 짝치환) \\ -1 & (\delta : 홀치환) \end{cases}\)

  ---

  • 치환 $\delta$ 안의 임임의 두 수를 바꾼 치환을 $\tau$라 하자,
    \(sgn(\tau) = -sgn(\delta)\)
    ※ 치환에서 두 수의 순서가 바뀌면 부호가 바뀐다.

행렬식 (Leibniz Formula)

• 행렬 A=[$a_{ij}$]가 n차 정사각 행렬일 때, A의 행렬식( $det(A), |A|$ )의 정의 (Sarrus 방법)
  \(det(A) = |A| = \sum_{\delta \in S_n} {sgn(\delta)a_{1 \delta(1)}a_{2 \delta(2)} \dots a_{n \delta(n)}}\)
  
  ※ 행렬 A의 행과 열에서 중복없이 하나씩 뽑아서 곱한 후 대응되는 치환의 부호를 붙인 것.

  ---

  • 1차 정사각 행렬 A=[$a_{11}$]의 행렬식은 $det(A)=a$이다.
  • 4차 이상의 행렬식엔 적용할 수 없다.

  ---

  행렬식의 성질

  1. $det(A) = det(A^T)$
  2. 행렬 $B_{n \times n}$이 행렬 $A_{n \times n}$의 두 행(열)을 서로 바꾸어서 얻어진 행렬이라면, $det(B) = -det(A)$ 이다.
  3. 행렬 $A_{n \times n}$의 두 행(열)이 일치하면, $det(A) = 0$ 이다.
  4. 행렬 $A_{n \times n}$의 한 행(열)의 성분이 모두 $0$이면, $det(A) = 0$ 이다.
  5. 행렬 $A_{n \times n}$의 한 행을 $k$배하여 얻어진 행렬을 $B$라 하면, $det(B) = kdet(A)$ 이다.
  6. 행렬 $A_{n \times n}$의 두 행이 비례하면, $det(A)=0$ 이다.
  7. 행렬 $A_{n \times n}$의 한 행의 $k$배를 다른 행에 더하여 얻어진 행렬을 $B_{n \times n}$라 하면, $det(B) = det(A)$이다.
  8. 행렬 $A_{n \times n}$가 n차 삼각행렬이면, $det(A)=a_{11}a_{22}a_{33}$ \dots a_{nn}$(주대각성분의 곲) 이다.
  9. $det(AB) = det(A)det(B)$

  ---

  기본행렬(Elementary Matrix)의 행렬식

  1. $E$가 $I_n$의 한 행에 $k(k\ne0)$을 곱한 것이면, $det(E)=k$ 이다.
  2. $E$가 $I_n$의 두 행을 서로 바꾼 것 이면, $det(E)=-1$ 이다.
  3. $E$가 $I_n$의 한 행에 $k$배하여 다른 행에 더한 것 이면, $det(E)=1$ 이다.
  4. $E$가 n차 기본행렬이면, $det(EA) = det(E)det(A)$ 이다.

가역행렬의 행렬식

• 행렬 $A_{n \times n}$가 가역행렬일 필요충분조건
  \(det(A) \ne 0\)

  행렬 $A_{n \times n}$가 가역이면 $det(A)=0$ 이고, $det(A^{-1})= \frac{1}{det(A)}$ 이 성립한다.

2. 여인자 전개와 행렬식의 응용

소행렬식(minor)과 여인자(codactor)